AWSでデータ分析基盤を構築してみよう
今回は、AWS(Amazon Web Services)が提供するクラウドコンピューティングサービスを利用したデータ分析基盤の構築例と関連するいくつかのサービスをご紹介したいと思います。
まずは、データ分析基盤とは何かを簡単にご説明していきます。
データ分析基盤とは
データ分析基盤とは、データを収集、蓄積、加工、分析・可視化するための基盤です。
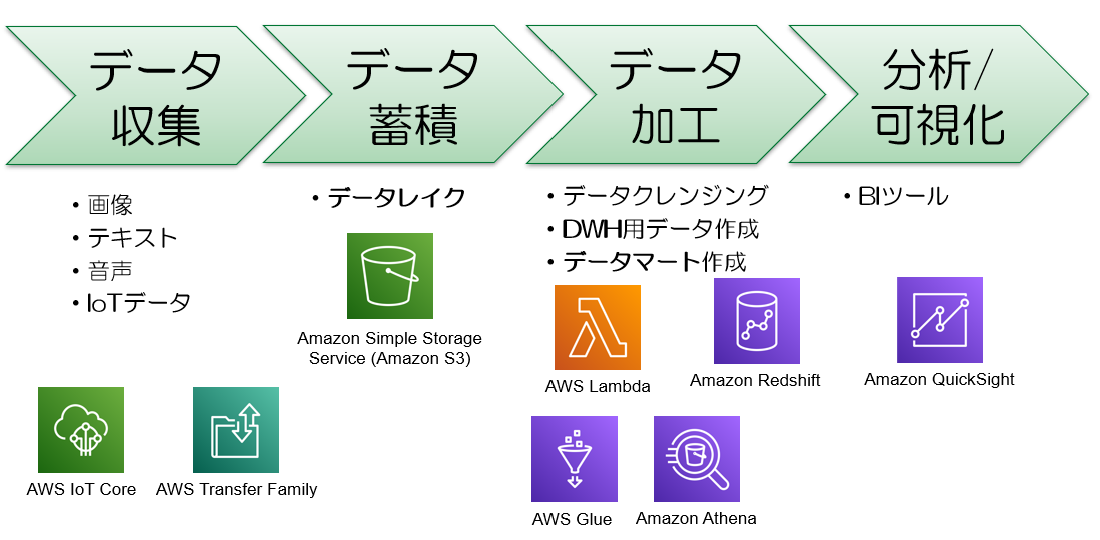
Amazon S3:データレイクとしても利用できるストレージサービス
AWS Lambda:サーバーレス環境でデータ処理が可能
Amazon Redshift:データウェアハウス
AWS Glue:データのETL(抽出、変換、ロード)を行う
AWSには上記以外にも200以上のさまざまなサービスが用意されており、これらのサービスを組み合わせることで、要件にあったデータ分析基盤を構築することができます。
データ分析基盤の構成例に入る前に、データを蓄積するデータレイクについて、関連するデータウェアハウス、データマートと一緒に整理しておきます。
データレイク、データウェアハウス(DWH)、データマートの比較
データレイクは、大量のデータをそのままの形式で格納・保管するデータストレージで、AIモデルの学習や予測のためにも使用されます。
CSV形式のような構造化データはもちろん、JSON、XML、画像、音声、動画など様々な形式のデータを時系列に蓄積していくため、大容量のストレージが必要となります。
また、データレイクに格納するデータは、必ずしも利用目的が明確になっている必要はありません。
対して、データウェアハウスには利用目的に合わせた構造化データとして保管し、さらに特定の目的に合わせて最適化したデータがデータマートとなります。

AWSで構築するデータ分析基盤の構成例
データレイク、データウェアハウス、データマートをAmazon S3で実現するシンプルな構成例です。
データ加工は、AWS LambdaやAWS Glue、データの可視化、分析はAmazon QuickSightを利用します。

以降で、使用しているAWSサービスの特徴をみていきます。
Amazon S3
Amazon S3には、以下のような特徴があります。
- 容量が無制限
- 低コスト(0.023USD/GB) ※東京リージョン、標準ストレージ
- イレブンナイン(99.999999999)の耐久性
- 99.9%の可用性
- AWSサービスとの連携が容易
- 暗号化によるセキュリティ強化
これらの特徴より、Amazon S3はデータレイクとして非常に適したサービスと言えます。
AWS Lambda
AWS Lambdaには、以下のような特徴があります。
- サーバレス
- マルチリージョンで高可用性を維持
- オートスケーリング
- 従量課金
- 15分を超える処理は実行できない
サーバー構築やアプリケーションのインストールといった環境構築は不要で、PythonなどのコードでLambda関数を作成するだけで、簡単に作成した処理を実行することができます。ただし、15分以上の処理を実行したい場合は、次に紹介するAWS Glueなどの別サービスを検討する必要があります。
また、Amazon S3のイベント通知やAmazon EvnetBridgeと組み合わせることで、特定のイベントが発生したタイミングでLambda関数を実行させることが可能です。
AWS Glue
AWS Glueには、以下の4つの機能があります。
Glueジョブ
データの抽出、変換、ロードを行います。 AWS Glue Studioを利用しノーコードでジョブを作成することができますし、Python、またはScalaで処理を書くこともできます。
データカタログ
データカタログは、データベース、テーブル、スキーマ情報で構成されています。
クローラー
Amazon S3などのデータストアに格納されているデータからデータカタログを作成します。
ワークフロー
GUIでクローラー、ジョブ、トリガーと呼ばれるノードを組み合わせ、ワークフローを定義することができます。
トリガーには、ワークフローの起動条件となる開始トリガーとGlueジョブやクローラーの開始条件を定義するトリガーがあり、例えば、毎日00:00時にワークフローを起動し、クローラーAとクローラーBの処理が完了したらジョブABを実行させるといった定義を行うことが可能です。
Amazon QuickSight
Amazon QuickSightには、以下のような特徴があります。
- フルマネージドのBIサービス
- ユーザーロール種類
- SPICEと呼ばれるインメモリを持つ
- 料金
- Admin、Author:24USD/月(SPICE容量10G無料枠付き)
- Reader:セッション数による従量課金(最大5USD/月)
- アセット(データソース、データセット、ダッシュボード、分析)のアクセス管理機能
データソースとしてAWS Athenaを利用し、Amazon S3のデータをSQLクエリで操作した結果を取り込むこともできます。
AWS TransferFamily
AWS TransferFamilyには、以下のような特徴があります。
- フルマネージドサービス
- SFTPサーバーサーバ、FTP/FTPSサーバを構築できる
- SFTP、FTPS、FTPプロトコルを使用した転送を行えるサーバを構築できる
- Amazon S3、Amazon EFSにファイルを転送することができる
- ワークフロー機能を利用し、データが転送されたタイミングの処理を定義することができる
今回は、SFTPプロトコルを利用した公開鍵認証を使った転送を行いました。SFTPクライアントとしてはWinSCP、Cyberduck などが利用可能です。
まとめ
AWSを利用するメリットとしては、すぐに始められるところだと思います。
要件が確定していない場合でも、最初はスモールスタートで構築し、必要に応じてサービスを追加、または変更していくことをお勧めします。
注意点としては、AWSの多くのサービスが従量課金ということです。利用するサービスの料金体系については、AWSのドキュメントやコスト見積ツール(AWS Pricing Calculator)を利用するなど、事前に確認したうえで構築を始めていきましょう。
calculator.aws
画像生成AIを試してみた
昨今、AI(人工知能)は私たちの生活に大きな変化をもたらしています。
AI技術は急速に進化し、日常からビジネス、医療、エンターテインメントまで、
様々な分野で活用されている場面をよく見かけるようになりました。
今回は、そのようなAI技術の1つである、画像生成AIについてお話しします。
画像生成AIについてよく分からない、試しにAIで画像を生成してみたいという方に向けて、
概要から、実際にツールを使用してAIで画像を生成してみるところまでをご紹介いたします。
画像生成AIについて
画像生成AIの流れを簡単にご説明しますと、「こうゆう画像がほしい」と思ったイメージに合わせてワードを入力すると、入力したテキストに沿ったイメージ画像をAIが自動で生成してくれるといったシステムです。
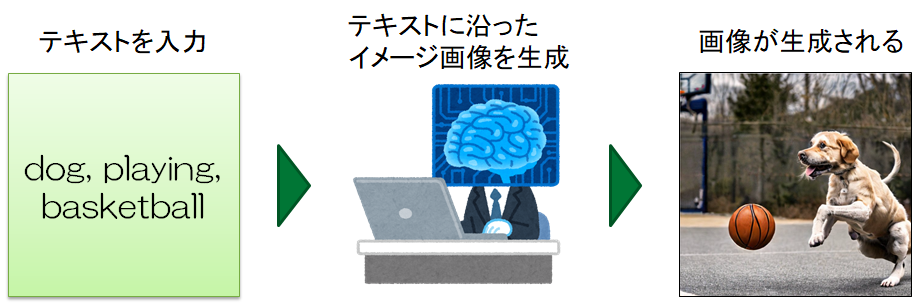
「dog, playing, basketball」のようにイメージに合うワードをカンマ区切りで繋げて入力します。
すると、実際に上記右の写真が生成されました。
メリット・デメリット
画像生成AIには沢山のメリットがありますが、デメリットもあります。
メリット
欲しい画像の特徴を伝えると、数秒でハイクオリティな画像が生成される
イラストやデザインを自分で作成しようと思うと時間がかかります。画像生成AIを使用すれば、「こんな画像が欲しい」と思ったら、そのイメージに合ったテキストを入力するだけで数秒~数十秒程度で画像ができてしまいます。
存在しないシチュエーションなど、ユニークな画像が生成できる
前述で「バスケットボールをしている犬」のように普段見られない光景だったり、シチュエーションを生み出すことができるのも魅力の1つです。
作業の効率化
資料作成やWebサイト制作など、画像が必要になるシチュエーションは多くあるでしょう。そういった際、欲しい画像をテキスト入力だけでパッと作れてしまえば、作業時間を大幅に短縮できます。
様々なタッチのデザイン生成が可能
画像生成AIはアニメ風だったり、写真風だったり、さらには背景など、様々なタッチの画像生成が可能なため、様々なパターンでアイデアを膨らませることができます。
デメリット
画像の品質が不安定
生成した画像の中には、ぼやけてしまったり、不自然だったりと必ずしも品質が一定ではありません。ですが、AI技術は急速に成長を進めているため、より進化していくことでしょう。
著作権の侵害問題
画像生成AIで特に注目されているのが、著作権の問題です。生成された画像が既存の著作権や知的財産権を侵害しないか注意する必要があります。今後、法整備がしっかり整うまで色々と問題が発生しそうですね。
日本語対応が少ない
画像生成AIサービスのほとんどは英語対応となっており、指示するワードを英語で入力する必要があります。日本語対応のサービスも存在はしておりますが、翻訳ツールを使うことも1つの手としてこの問題は回避できますね。
フェイク画像などの悪用
法整備が不完全なこともあり、AIで生成した画像を使用して悪用するケースが発生しています。特に災害の様子のフェイク画像が流出し、多くの人が勘違いしてしまうことが過去に起きています。よく見ると不自然な部分があり、フェイク画像だと判断されていますが、画像の精度も上がってきているため、ますます見分けがつかなくなってしまいます。自分でしっかり情報収集し、見分けられる力が必要になってきます。
活用方法
画像生成AIはどのような場面で活用されているのでしょうか。
独自のイラストが欲しくても、絵を描くことが苦手だったり、アイデアが浮かばなかったり、、、
そんな時にすぐにオリジナルの画像を生成してくれるのはとても魅力的です。
上記はほんの一部で、他にも様々な場面で活用されています。
趣味として楽しんだり、ビジネスの中で作業の効率化として活用したり、医療現場でも活用されているようで、今後さらに画像生成AIの注目が集まりますね。
実際に画像生成AIで画像を生成してみた
今回、以下の手順で画像生成AIを試してみました。
使用するツール
手順
①Paperspaceで仮想環境を作成する
②Stable Diffusion Web UIとモデルの追加
手順① Paperspaceで仮想環境を作成する
まず、Stable Diffusion Web UIで画像生成AIを使うために、2種類の方法があります。
1つはハイスペックなPCを用意すること、もう1つはクラウドサービスを利用することです。
前者の場合、特に重要なのが、画像処理を行うGPUのスペックとして、VRAM12GB以上が推奨されています。
今回は、誰でも実現できるよう、後者のクラウドサービスを利用してみました。
利用したクラウドサービスは、定額制で使い放題の「Paperspace」というものです。
まずは、上記ログイン画面からPaperspaceの登録をします。
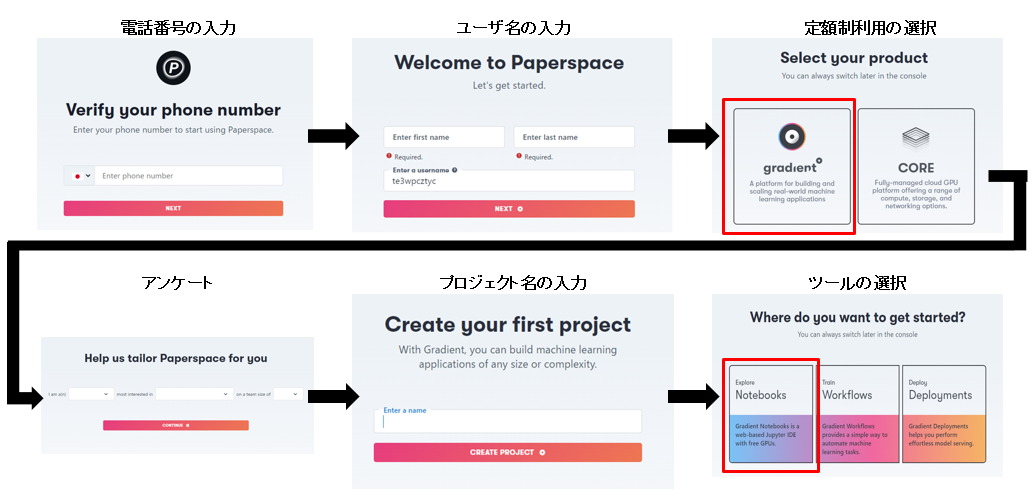
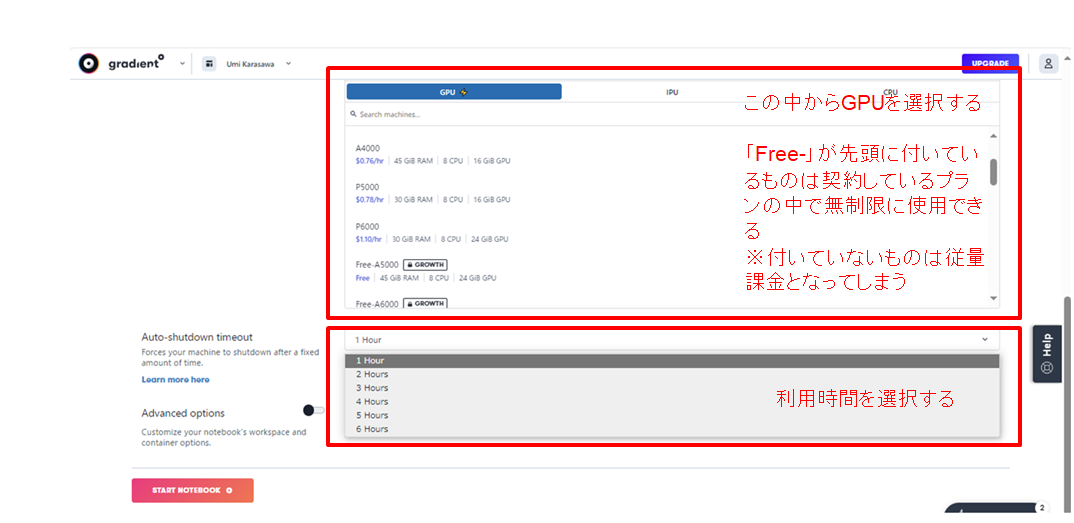
登録が完了したら、Notebooksを作成し、GPUをレンタルします。
「Start from Scratch」を選択し、
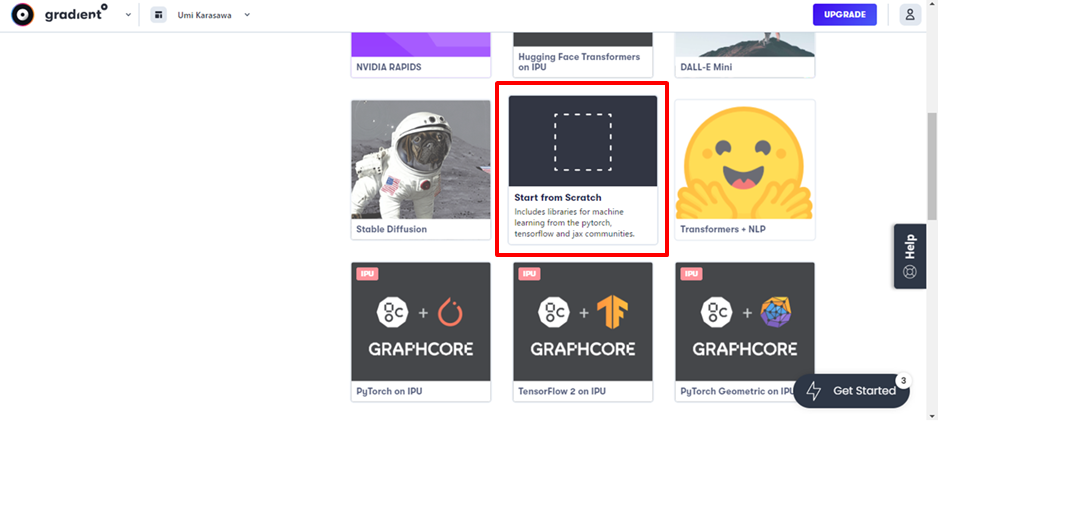
あとは、利用時間を選択できます。ここでいう利用時間は自動でシャットダウンされてしまう時間です。時間を過ぎてしまった場合は、再度借りなおせば、続けて使用できます。
手順② Stable Diffusion Web UIとモデルの追加
PaperspaceにStable Diffusion Web UIとモデルを追加していきます。
Github上にPaperspaceのテンプレートがあるのでダウンロードしてきます。
上記Githubからテンプレートをダウンロードし、Paperspaceにアップロードすると下記の画像のように、コマンドが4つに分類されています。それぞれ一番上にコメントで番号がふられているため、順番に実行していくと、Stable Diffusion Web UIとモデルの追加が完了します。

一番上の「#(3) WebUI起動」を実行すると、Stable Diffusion Web UIのパブリックのURLが表示されるため、クリックします。

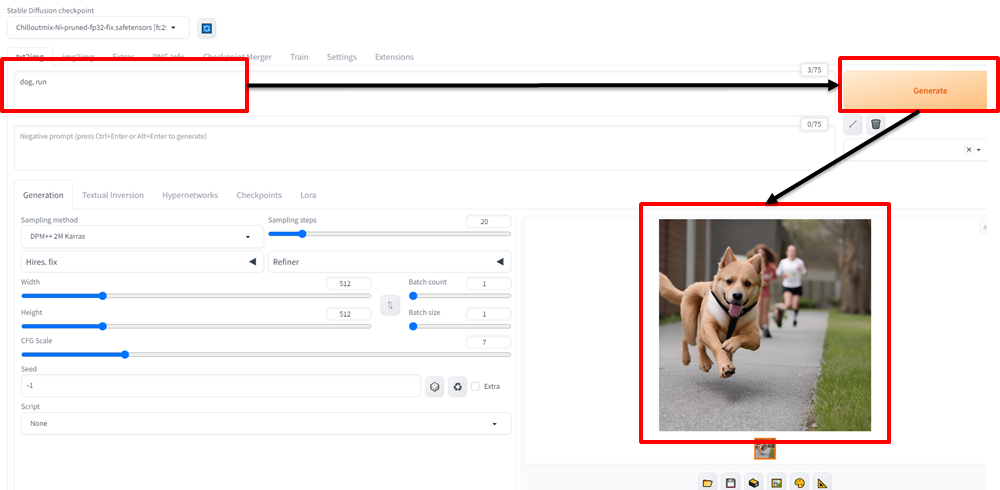
試しに、「犬が走っている画像」⇒「dog,run」と入力し、Generateボタンを押下すると下記の図のような犬がこちらに向かって走ってくるような画像が生成されました!
ちょこっとAIで画像生成してみたいという場合は無料で簡単に試すことができるサイトもあります。さらに幅広く、画像生成AIを無制限で使いたい、追加学習させてみたいなど、新たな可能性を広げたい場合に、高性能なPCを持っていないという方はぜひ参考にしてみてください。
まとめ
今回は、画像生成AIについてお話ししました。
まだまだ、豊富な設定項目だったり、モデルだったり、様々な機能が存在するため、そういった機能を駆使することで、生成画像の幅がもっと広がります。
本記事で少しでもご興味を持ってくださいましたら、ぜひ画像生成AIを試してみてください。
ページネーションについて
今回は、ページネーションについて解説します。
最初に
検索結果一覧など、ユーザーに対して複数のコンテンツを一度に表示する手段として、リストが挙げられます。 しかし、利用できるコンテンツが膨大なのに対して、端末で表示できるコンテンツ数はごく小さいことがあります。その場合、一度にすべてのコンテンツを読み込むと、UI/UX を損ない、また端末のリソースを無駄に消耗します。 今回、この問題の解決手段として、ページネーションを説明します。
対象範囲
今回は、ページネーションの概要と実例、そして実装例を説明します。また、ページネーションはモバイルアプリにて利用されることが多いため、Android アプリを例にして説明します。 なお、サーバーサイドにおけるページネーションの実装については省略します。
ページネーションとは?
ページネーションとは、複数のコンテンツを適度な長さに区切って複数ページに分割する機能です。
例えばモバイルアプリの場合、
サーバーに保存されているコンテンツをダウンロードして表示する場合、すべてのコンテンツを一度に全部ダウンロードすると要領が悪い。
複数ページに分割してダウンロードすることにより、効率的にアプリを動かすことができる。
実例
ページネーションの実例を示します。
以下は、Google ブックスアプリにおけるページネーションの実例です。

実装
今回は、Google Books APIs から取得した書籍情報をページネーションで表示する説明をします。
Google Books APIs
Google Books APIs とは、Google ブックスにある情報を取得できる WebAPI です。 以下に、WebAPIの呼び出し例とその結果を記載します。
呼び出し例
https://www.googleapis.com/books/v1/volumes?q=android&maxResults=30&startIndex=0
結果
{ "kind": "books#volumes", "totalItems": 1387, "items": [ { "kind": "books#volume", "id": "hkfWnQEACAAJ", "etag": "/u9dh+5dqEU", "selfLink": "https://www.googleapis.com/books/v1/volumes/hkfWnQEACAAJ", "volumeInfo": { "title": "Andoroido no nakami", "subtitle": "", "authors": [ "Tae Yeon Kim", "Hyung Joo Song", "Hoon Park Ji" ], "publishedDate": "2013-12", "description": "Androidの内部構造を徹底解剖。ソースコードの分析を通してAndroidフレームワークの全貌に迫る。", // 省略 }, // 省略 } ] }
説明
URL:https://www.googleapis.com/books/v1/volumes
| No. | クエリ | 説明 |
|---|---|---|
| 1 | q | 検索語句 |
| 2 | maxResults | 1 ページあたりの最大件数 |
| 3 | startIndex | startIndex:検索結果の開始位置(startIndex=0,1,2,3,…) |
以上より、リストを一番下までスクロールするたびに、startIndex を +1 して API を呼び出せばよいことがわかります。
Paging ライブラリ
Android には、Paging というページネーションの実装を簡略化するライブラリが存在するので、それを使用します。
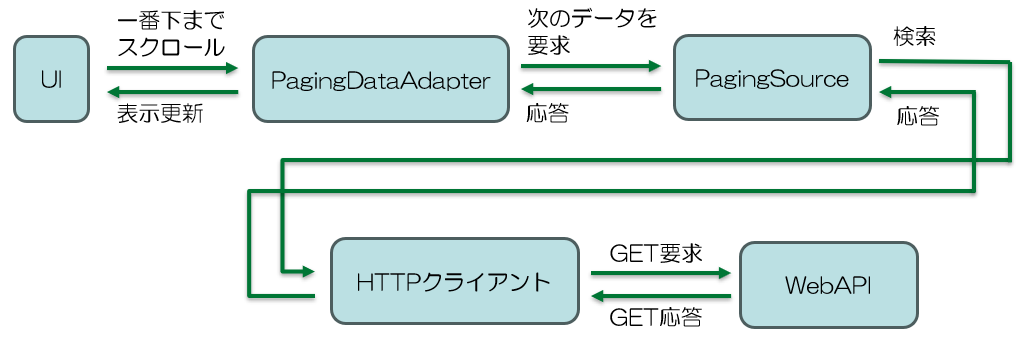
概念図
以下に、Android の Paging ライブラリの概念図を示します。
build.gradle
以下のライブラリを追加します。
dependencies {
// Paging ライブラリ
implementation "androidx.paging:paging-runtime:3.2.0"
implementation "androidx.paging:paging-rxjava3:3.2.0"
implementation "io.reactivex.rxjava3:rxjava:3.1.6"
implementation "io.reactivex.rxjava3:rxandroid:3.0.2"
// リスト表示
implementation "androidx.recyclerview:recyclerview:1.3.1"
// HTTP クライアント
implementation "com.squareup.retrofit2:retrofit:2.9.0"
implementation "com.squareup.retrofit2:adapter-rxjava3:2.9.0"
implementation "com.squareup.retrofit2:converter-moshi:2.9.0"
implementation "com.squareup.moshi:moshi:1.15.0"
}
HTTP クライアント
以下の通り、HTTP クライアントを宣言します。
public interface GoogleBooksApisService { /** * 書籍を検索する。 * * @param query 検索語句 * @param maxResults 1ページあたりの最大件数 * @param startIndex 検索結果の開始位置 */ @GET("books/v1/volumes") @NonNull Single<Books> searchBooks(@Query("q") @NonNull String query, @Query("maxResults") int maxResults, @Query("startIndex") int startIndex); }
PagingSource
実際に WebAPI を呼び出す Paging ライブラリのクラスです。 PagingDataAdapter から要求されるたびに、インデックスを +1 加算して WebAPI を呼び出し、その結果を返します。
実装では、RxPagingSource を継承して、loadSingle をオーバーライドします。
public final class GoogleBooksPagingSource extends RxPagingSource<Integer, Item> { @NonNull @Override public Single<LoadResult<Integer, Item>> loadSingle( @NonNull final LoadParams<Integer> loadParams ) { // リストが一番下までスクロールされたときなどに呼び出される。 // WebAPIの呼び出しを実装する。 } }
RxPagingSource#loadSingle
WebAPI の呼び出しを実装します。
@NonNull @Override public Single<LoadResult<Integer, Item>> loadSingle( @NonNull final LoadParams<Integer> loadParams ) { // LoadParams#getKey()から次のインデックスを取得できる。 final Integer key = loadParams.getKey(); final int startIndex; // 次のインデックスがnullの場合、先頭番号0で初期化する。 if (key == null) { startIndex = 0; } else { startIndex = key; } // WebAPIを呼び出す return service.searchBooks(query, 20, startIndex) // ワーカースレッドで呼び出す。 .subscribeOn(Schedulers.io()) // 応答から必要な結果を取り出す。 .map((books) -> toLoadResult(books, startIndex)) // エラーハンドリング .onErrorReturn(LoadResult.Error::new); }
GoogleBooksPagingSource#toLoadResult
次のインデックスの加算と、WebAPI の応答からの必要な結果の取り出しを行います。
@NonNull private LoadResult<Integer, Item> toLoadResult(@NonNull final Books books, final int startIndex) { final List<Item> items = books.getItems(); final Integer nextKey; // 次のインデックスを決定する。 if (items.isEmpty()) { // データが空の場合には、nullにする。 nextKey = null; } else { // データが空でない場合には、インデックスを+1加算する。 nextKey = startIndex + 1; } // 読み取り結果を返す。 return new LoadResult.Page<>( items, null, nextKey, // 読み取り結果に次のインデックスを格納する。 LoadResult.Page.COUNT_UNDEFINED, LoadResult.Page.COUNT_UNDEFINED ); }
PagingDataAdapter
UI のリスト表示とデータをつなぐ Paging ライブラリのクラスです。 リストが一番下までスクロールされたことを検出して、新しいデータ要求します。 また、WebAPI 呼び出しの状態(読み取り中や読み取りエラーなど)を保持しているため、その状態を取得して、UI にローディング画面やエラー画面を表示することができます。
実装では、PagingDataAdapter を継承して、必要なメソッドをオーバーライドします。
public final class GoogleBooksAdapter extends PagingDataAdapter<Item, GoogleBooksAdapter.ViewHolder> { @NonNull @Override public ViewHolder onCreateViewHolder(@NonNull final ViewGroup parent, final int viewType) { // ViewHolderを生成する。 } @Override public void onBindViewHolder(@NonNull final ViewHolder holder, final int position) { // ViewHolderにデータをバインドする。 } }
参考
Google Maps PlatformをVue.jsで使ってみる
今回はGoogle Maps PlatformをVue.jsで使用する例を紹介します。 この記事は、Vue.jsで少しでも実装したことがある方が対象です。
目標はVue.jsでGoogle Maps Platformを使用して、指定の緯度経度に対する周辺の地図を表示する以下のようなWebアプリを作成することです。
 |
環境については以下の通りです。
- Vue.js:3.2.13
- Google Maps Platform:2023/6/14時点のページ
Google Maps Platformとは?
そもそもGoogle Maps Platformは地図機能のAPIを提供するGoogle社のSaaSです。 世界中の方がGoogle Mapを使用していますし、これを読んでいる方も一度は使用したことがあるのではないでしょうか?
Google Maps Platformについて少し解説すると、個人の開発で使用する場合、月200ドル分まで地図やストリートビューの表示やルート検索など様々なAPIを使用することができます。 200ドル分とは、地図の表示で10万回分のため、月のアクセス数が多いと無料枠をすぐに超えます。注意してください。
さて、ここからは手順に沿ってアプリの作成をしていきましょう!
Google Maps Platform使用の設定をする
Googleアカウントを登録しGoogle Maps Platformのページを開く
まずはGoogleのページからアカウント登録を行います。すでにAPIを使用するアカウントを持っている方はこのアカウント登録の手順は必要ありません。
次に以下のURLからGoogle Maps Platformのページを開き、「使ってみる」をクリックします。
表示されたページで、国の選択や利用規約への同意を行うことで以下のようなページが表示されれば完了です。
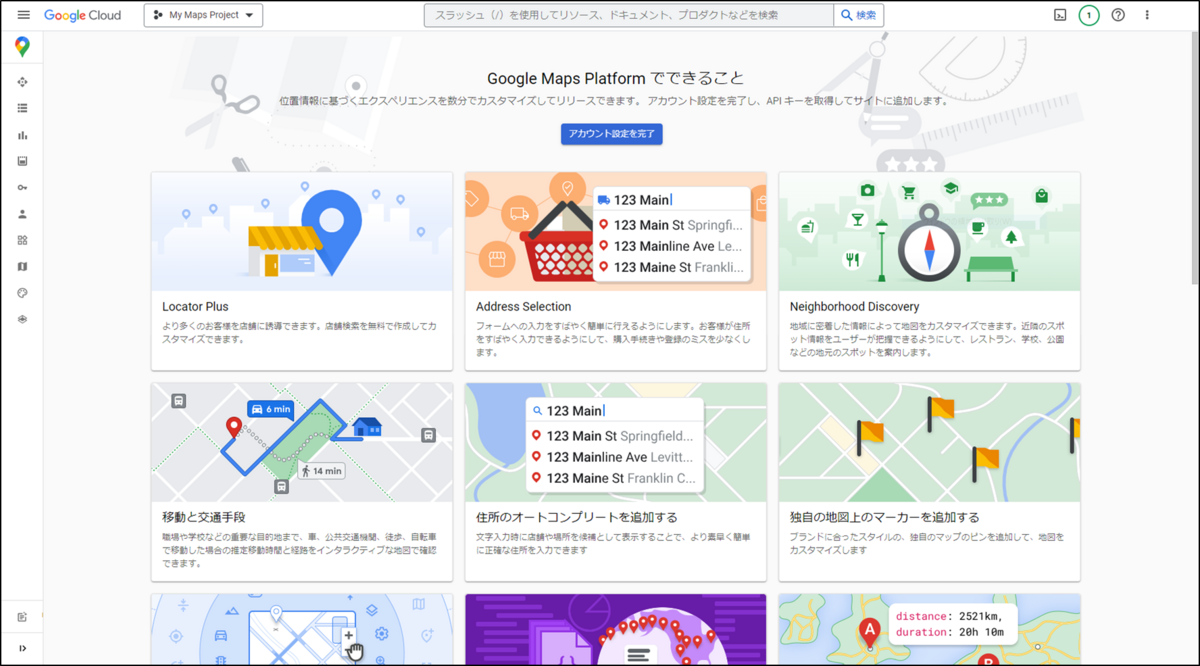
APIを使用するための設定を行う
APIを使うにはプロジェクト作成とクレジットカード情報の登録が必要です。 まずはプロジェクトを作成するには、以下の左上のセレクトボックスを選択し、「新しいプロジェクト」をクリックします。
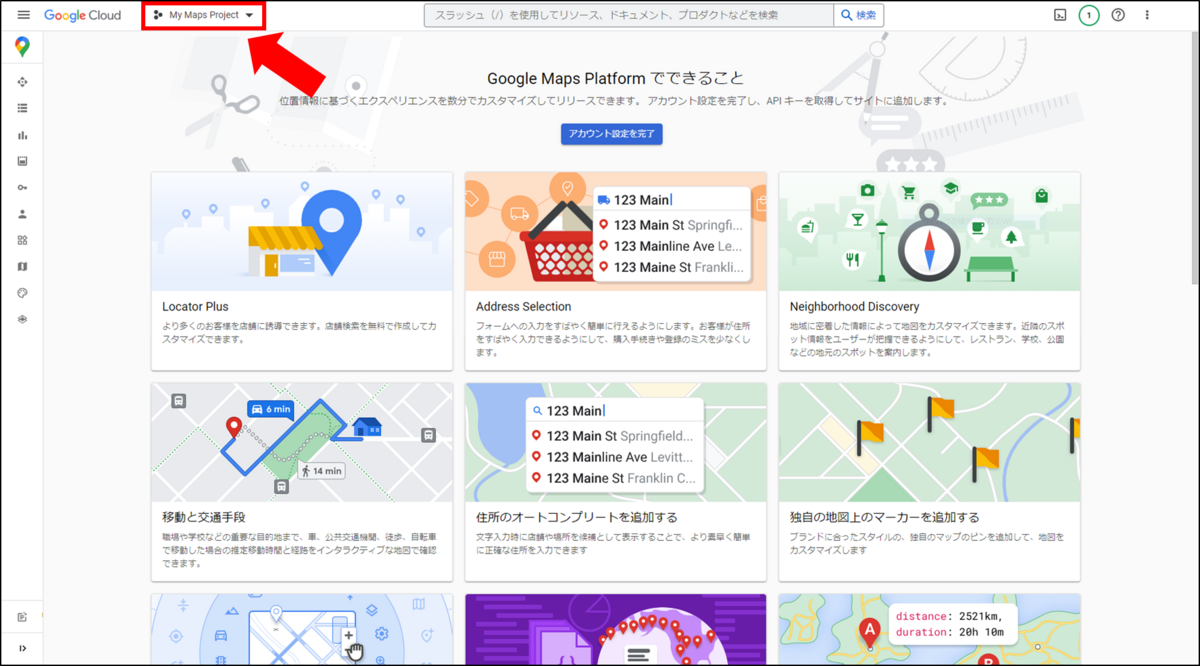
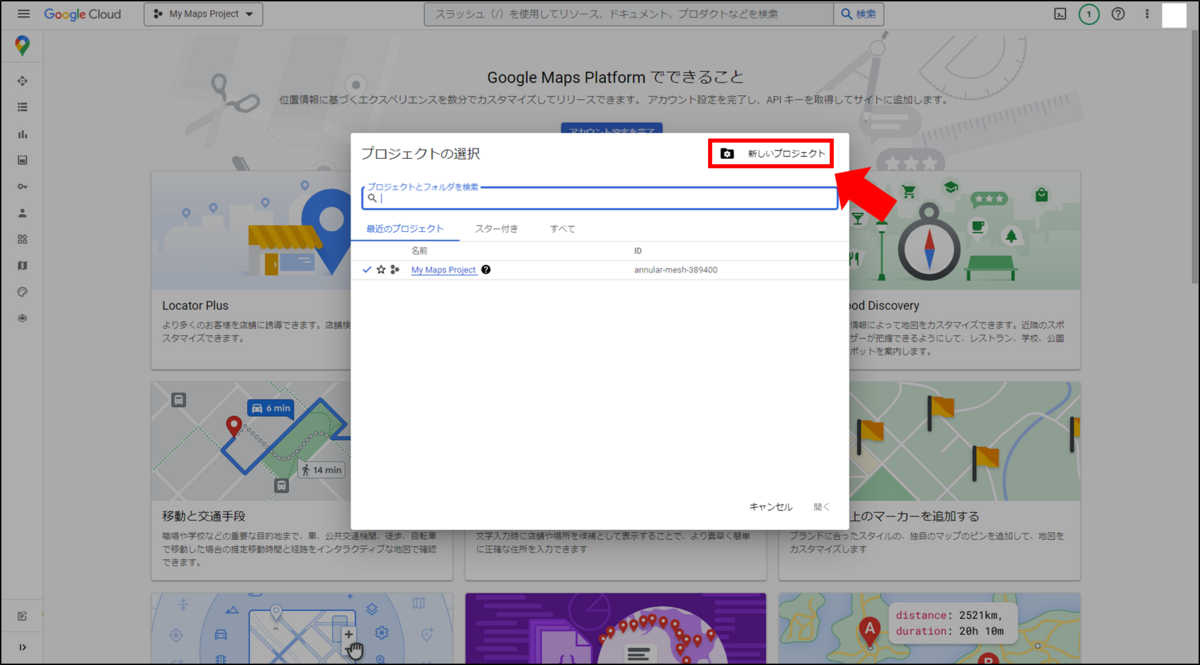
プロジェクト名を入れ「作成」をクリックします。右上の通知部分に作成のメッセージが出れば完了です。

次にAPIを使うための情報を入力していきます。先程作成したプロジェクトを表示するために、左上のセレクトボックスから作成したプロジェクトを選択します。

「アカウント設定を完了」をクリックし、ページに従って入力していきます。再度国の選択と利用規約への合意を行い、新しくクレジットカード情報の入力を行います。最後に「無料トライアルを開始」をクリックします。
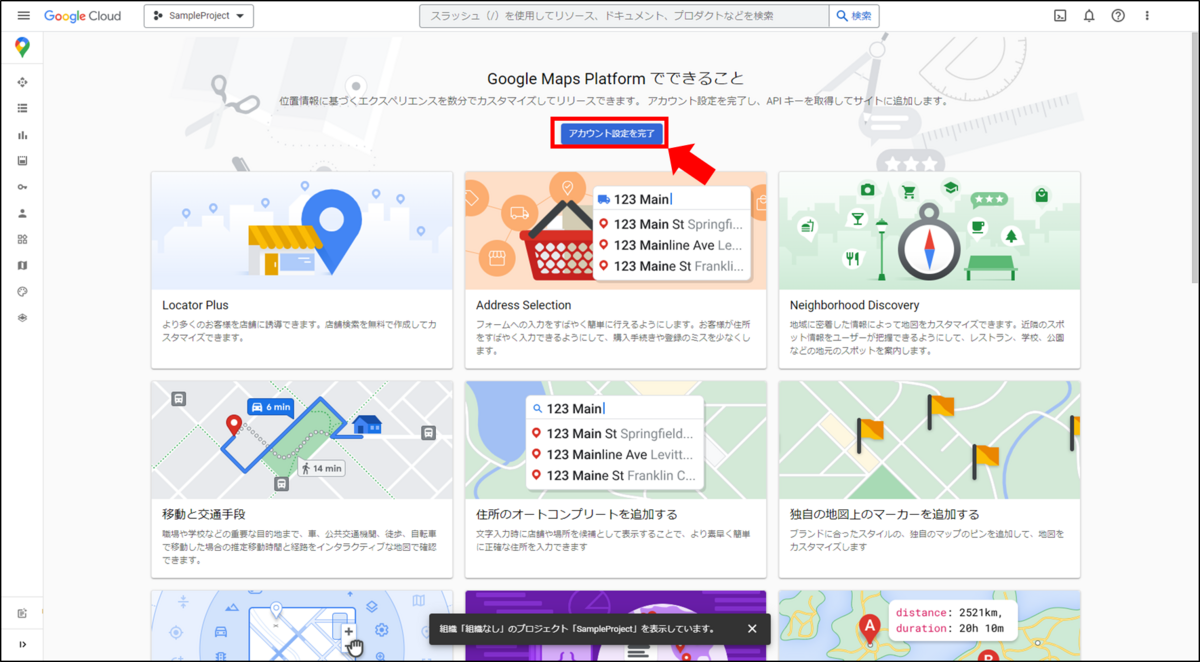
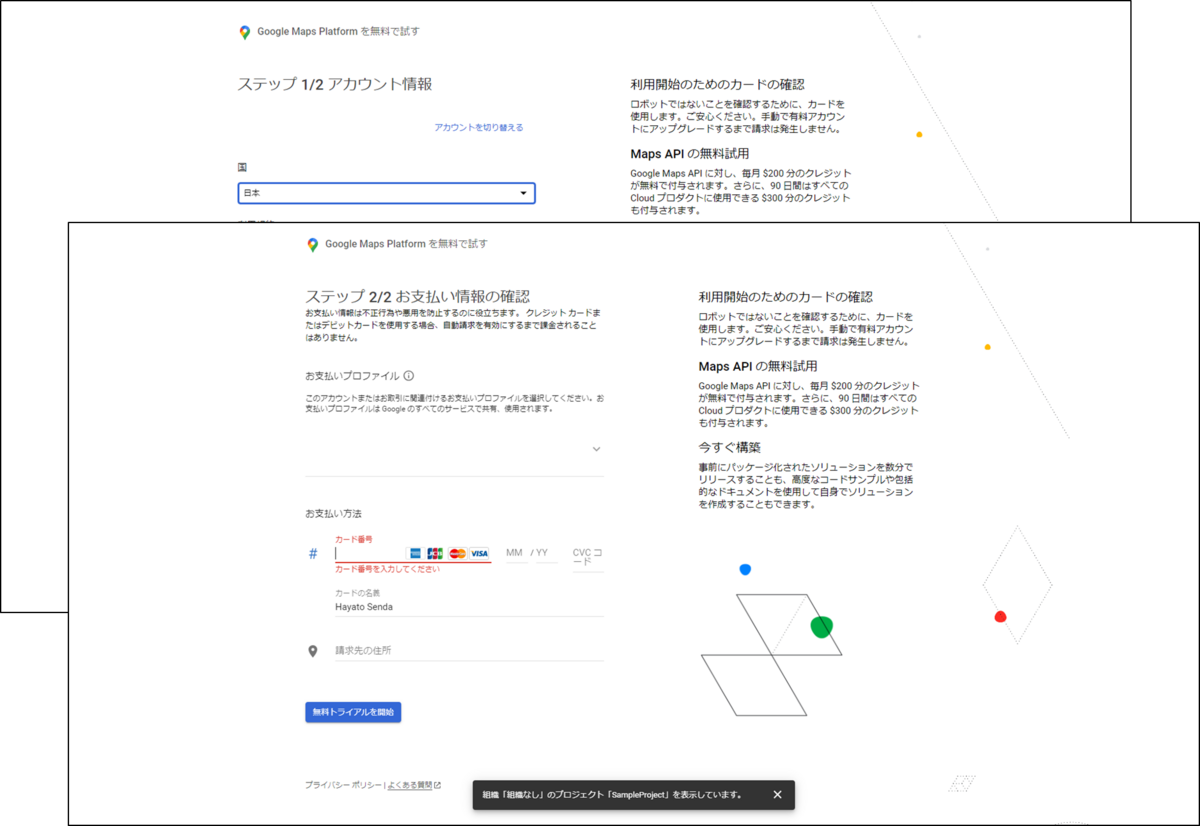
その後、使用する目的などいくつかの質問に回答し「送信」をクリックします。
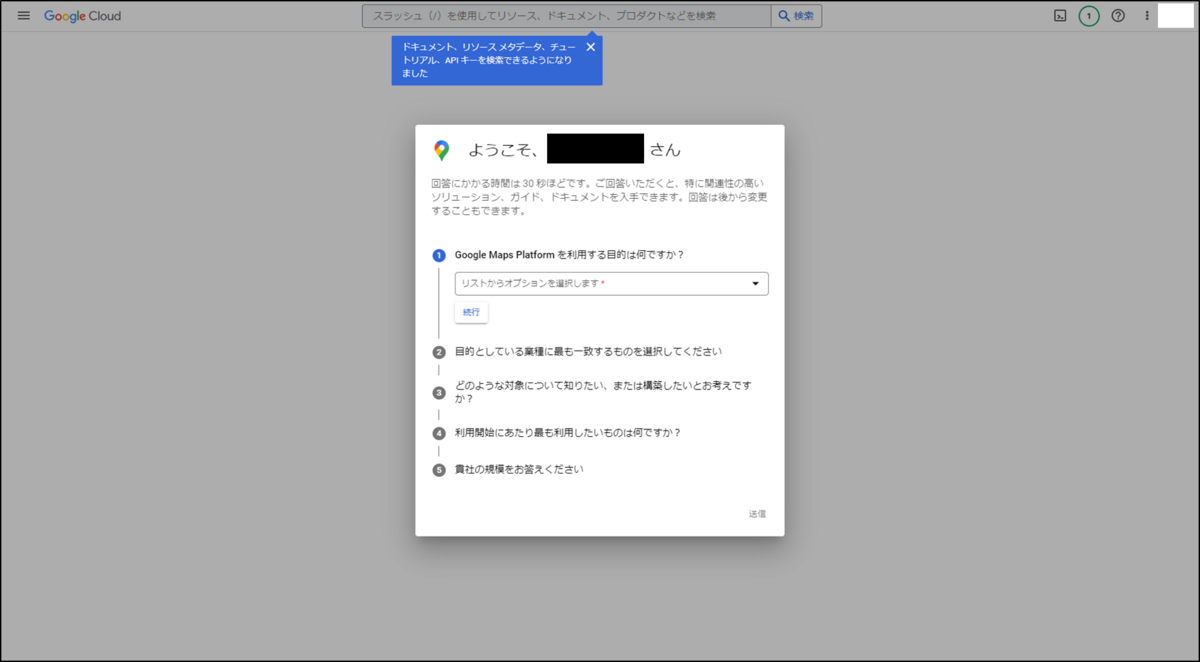
上記完了後、APIキーが表示されます。こちらは後でアプリ作成時に必要になるため、記録しておきます。
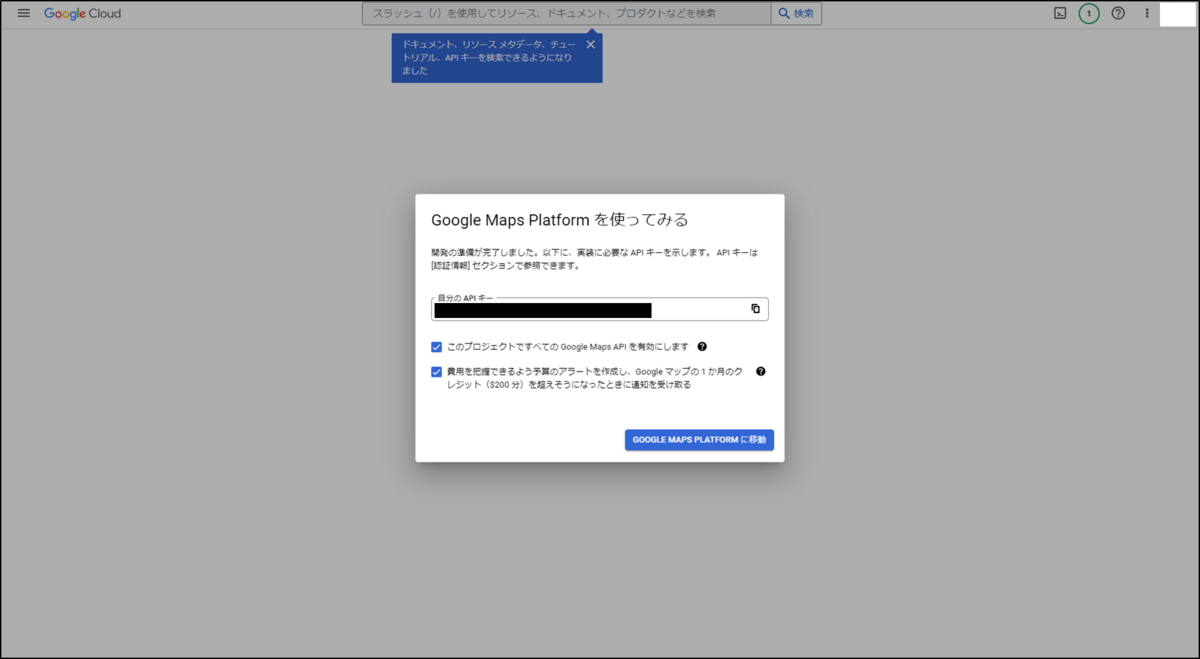
また、「GOOGLE MAPS PLATFORMに移動」をクリックするとAPIキー保護のダイアログが出ますが、後で設定可能なため、まずは「後で」をクリックします。これで完了です。
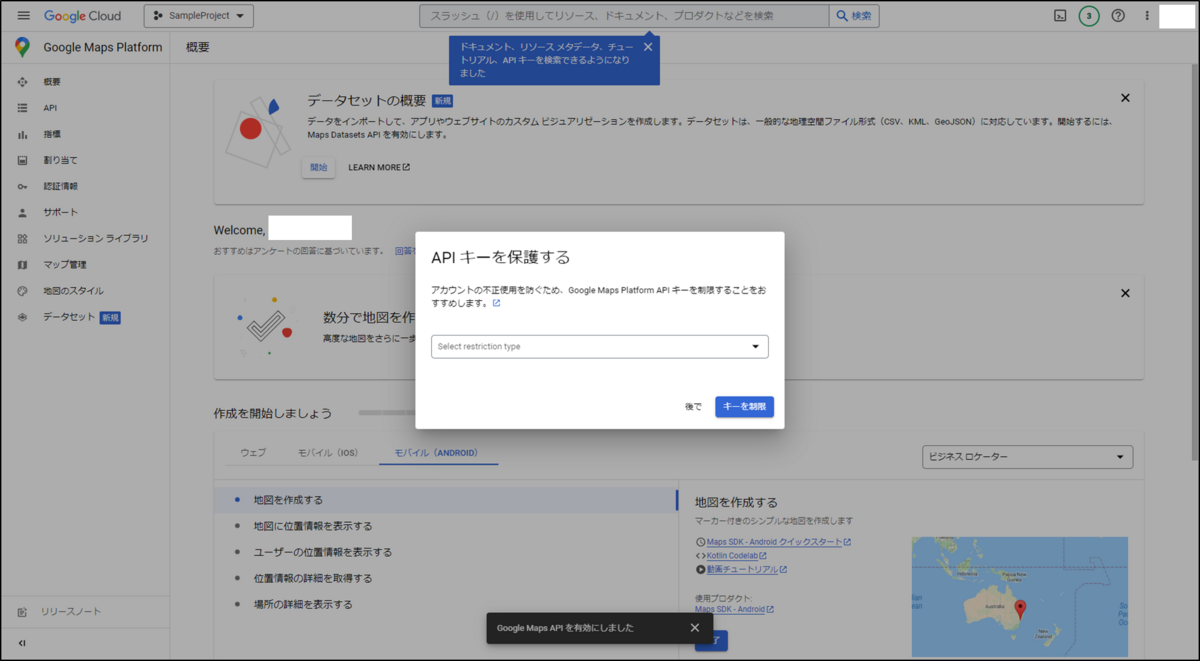
アプリを作成する
実装
続いてアプリですが、緯度経度を入力しボタンクリック後に地図を表示するアプリを作成します。
まずはVue.jsのCLIでプロジェクトを作成してください。ここでは作成手順は割愛するため、以下のようなページを参考に作成してください。また、RouterやVuexなどのプラグインはなくても今回のアプリは実装可能です。
肝となるページのコードは以下の通りです。こちらをプロジェクトのデフォルトで作成されるApp.vueの各タグ内に追記してください。
- template
<div> <form> <div> <label>Latitude: </label> <input type="text" v-model="latitude" /> </div> <div> <label>Longitude: </label> <input type="text" v-model="longitude" /> </div> </form> <button class="btn" style="width: 200px; background: skyblue;" v-on:click="showMap">SHOW</button> </div> <div ref="map" id="mapArea" style="height: 400px;"></div>
- script
data: () => ({ latitude: 35.46248486750884, longitude: 139.6231033539685, }), methods: { showMap() { // APIキーを使用しスクリプトの呼び出す const script = document.createElement('script'); script.src = 'https://maps.googleapis.com/maps/api/js?key=<APIキー>&callback=initMap'; script.async = true; document.head.appendChild(script); // スクリプト呼び出し後のコールバック window.initMap = () => { const myLatLng = { lat: Number(this.latitude), lng: Number(this.longitude) }; const map = new window.google.maps.Map(this.$refs.map, { center: myLatLng, zoom: 12, }); new window.google.maps.Marker({ position: myLatLng, map }); }; }, }
こちらのソースコードについて少し解説します。
templateの以下のコードは、地図が埋め込まれる部分ですが、枠幅をheight: 400px;などで指定しないと表示されないので注意してください。
<div ref="map" id="mapArea" style="height: 400px;"></div>
scriptの以下のコードは、Google Maps PlatformのAPIにアクセスする際に必要なスクリプトを読み込みます。 読み込むにはAPIキーが必要で、前の章で記録したAPIキーを入れることで実行が可能です。
script.src = 'https://maps.googleapis.com/maps/api/js?key=<APIキー>&callback=initMap'; script.async = true; document.head.appendChild(script);
動作確認
これで実装は完了です。実際に動かしてみると冒頭の画面のようになります。また、実際にAPIにアクセスしたことはGoogle Maps Platformの画面で確認できます。左メニューから「API」を選択することで確認可能です。
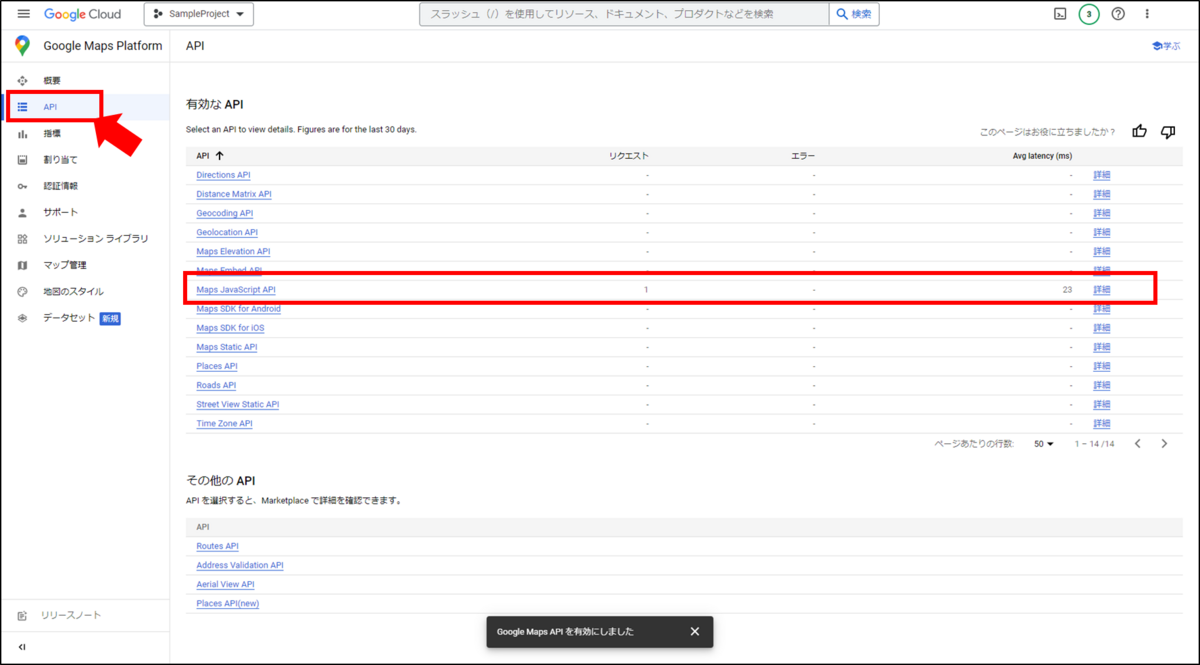
まとめ
さて、今回はGoogle Maps PlatformをVue.jsで使用する例について紹介しました。まとめると2つの手順でアプリを作成できます。
- Google Maps Platform使用の設定
- APIにアクセスするためのアプリ作成
紹介したような方法で簡単に実装できますが、Google Maps Platformには多くのAPIがあるため、活用方法は様々考えられます。
ぜひ使ってみてください!
【Kotlin】Kotlin Serialization で JSON をパースする
今回は、Kotlin Serialization を使って JSON をパースする方法を解説します。
なお、ここに掲載しているソースコードは以下の環境で動作確認しています。
- Android Studio Bumblebee | 2021.1.1 Patch 2
- JDK 11.0.11
- Android Gradle Plugin 7.1.2
- Kotlin 1.6.20
- Gradle 7.4.2
- org.jetbrains.kotlin.plugin.serialization 1.6.20
- org.jetbrains.kotlinx:kotlinx-serialization-json 1.3.2
ライブラリのインポート
最初に、Kotlin Serialization を使用するために必要なライブラリをインポートします。
まず、以下のようにプロジェクトの build.gradle の plugins に Kotlin Serialization のプラグインを追加します。
// Project's build.gradle plugins { id 'org.jetbrains.kotlin.plugin.serialization' version '1.6.20' apply false }
そして、モジュールの build.gradle の plugins にも Kotlin Serialization のプラグインを追加します。
// Module's build.gradle plugins { id 'org.jetbrains.kotlin.plugin.serialization' }
後は、モジュールの build.gradle の dependencies に以下を追加します。
// Module's build.gradle dependencies { implementation "org.jetbrains.kotlinx:kotlinx-serialization-json:1.3.2" }
以上で、ライブラリのインポートは完了です。
データクラスの宣言
ここから、実装に入っていきます。
まず、パースする JSON のフォーマットをデータクラスで宣言する必要があります。今回は、以下のような JSON の読み書きを行ってみます。
{ "hidden_card": { "rank": "6", "suit": "SPADES" }, "visible_cards": [ { "rank": "4", "suit": "CLUBS" }, { "rank": "A", "suit": "HEARTS" } ] }
上記の JSON をデータクラスで宣言すると、以下のようになります。
@Serializable data class BlackjackHand( @SerialName("hidden_card") val hiddenCard: Card, @SerialName("visible_cards") val visibleCard: List<Card>, ) @Serializable data class Card( val rank: Char, val suit: Suit, ) enum class Suit { CLUBS, DIAMONDS, HEARTS, SPADES; }
Kotlin Serialization で使用するデータクラスには、@Serializable を追加します。また、hidden_card と hiddenCard のように、JSON とデータクラスで名前が異なる場合、データクラスのプロパティに @SerialName を付与して、対応する JSON の名前を指定します。なお、JSON とデータクラスで名前が一致する場合は、@SerialName を省略できます。
以上で、データクラスの宣言は完了です。
JSON からオブジェクトにパースする
Json.decodeFromString に JSON 文字列を渡すと、パースした後のオブジェクトを返してくれます。
val json = """ { "hidden_card": { "rank": "6", "suit": "SPADES" }, "visible_cards": [ { "rank": "4", "suit": "CLUBS" }, { "rank": "A", "suit": "HEARTS" } ] } """.trimIndent() Log.d(TAG, Json.decodeFromString<BlackjackHand>(json).toString())
上記を実行すると Logcat に以下のログが表示され、JSON からオブジェクトにパースが成功していることがわかります。
D/MainActivity: BlackjackHand(hiddenCard=Card(rank=6, suit=SPADES), visibleCard=[Card(rank=4, suit=CLUBS), Card(rank=A, suit=HEARTS)])
オブジェクトから JSON にパースする
逆に、Json.encodeToString にオブジェクトを渡すと、パースした後の JSON を文字列で返してくれます。
val blackjackHand = BlackjackHand( Card('6', Suit.SPADES), listOf(Card('4', Suit.CLUBS), Card('A', Suit.HEARTS)) ) Log.d(TAG, Json.encodeToString(blackjackHand))
上記を実行すると Logcat に以下のログが表示され、オブジェクトから JSON にパースが成功していることがわかります。
D/MainActivity: {"hidden_card":{"rank":"6","suit":"SPADES"},"visible_cards":[{"rank":"4","suit":"CLUBS"},{"rank":"A","suit":"HEARTS"}]}